-
PDF
- Split View
-
Views
-
Cite
Cite
Hiro-Sato Niwa, Random-walk dynamics of exploited fish populations, ICES Journal of Marine Science, Volume 64, Issue 3, April 2007, Pages 496–502, https://doi.org/10.1093/icesjms/fsm004
Close - Share Icon Share
Abstract
Fished populations have been heavily fished over a wide range of stock sizes, and the data for such stocks are potentially of great interest. Population variability in stock histories has focused attention on the predictability of conditions of sustainability when harvesting fish. Here, I examine empirically the time-series data on 27 commercial fish stocks in the North Atlantic. The variability in population growth rate (i.e. the annual changes in the logarithms of population abundance) is described by a Gaussian distribution. The signs (up or down) of successive changes in the population trajectory are independent, as if determined by the toss of a coin. The process of population variability therefore corresponds to a geometric random walk.Niwa, H-S. 2007. Random-walk dynamics of exploited fish populations. – ICES Journal of Marine Science, 64: 496–502.
Introduction
Fluctuations in marine fish landings have been a concern for many years (Botsford et al., 1997; Pauly et al., 2002; Halley and Stergiou, 2005; Niwa, 2006a). The variation in supply (the stock size) is a central issue when fishery managers decide how best to regulate fishing effort. A fishery scientist's standard approach to trying to ensure sustainable harvesting is to identify the location of the stock-recruitment curve in relation to the replacement line defining the recruitment level needed to replace the spawning stock in future (Ricker, 1954; Beverton and Holt, 1957; Ulltang, 1980; Caddy and Sharp, 1986; Cook et al., 1997; Hjermann et al., 2004). The place where the two lines intersect is the equilibrium point to which the population is attracted. The resulting theory on sustainably harvesting fish stocks would be mathematically convenient for resource managers, but it fails abysmally to fit historical data on abundance (Shepherd and Cushing, 1990; Dixon et al., 1999). The fitted curves have been plagued by the extreme scatter of data points, and there is always doubt about the precise level of sustainability (Schnute and Richards, 2001; Longhurst, 2006). The term “equilibrium” may even be an empty concept. Despite substantial effort directed towards elucidating the population dynamics of exploited fish stocks, declines and recoveries in abundance remain an ecological enigma (Myers et al., 1995; Hutchings, 2000; Sibly et al., 2005). Characterizing temporal patterns in population size is a major challenge for ecological time-series analysis, especially attempting to show evidence or suggestions of the source of the variability.
Material and methods
Time-series data
Spawning-stock biomass (SSB) data are generally derived from sequential population analysis, which can lead to systematic error in the abundance computed. Because time-series results are the product of a quite complex and potentially biased estimation process (results for successive years are inferred on the basis of landed catches), they may be subject to change when data are tuned in various ways. Nevertheless, it is generally considered by scientists that there is good correspondence between time-series data and actual levels of population abundance.
Here, I extract information on the temporal variability in SSB from time-series data on commercial fish stocks in the North Atlantic. The data are derived from the 2005 working group reports of the International Council for the Exploration of the Sea (ICES), prepared to support advice on living resources and their harvesting provided by the ICES Advisory Committee on Fishery Management (ACFM). The information can be found at <http://www.ices.dk/advice/icesadvice.asp>. I select from the database those stocks for which the annual time-series of SSB encompassed at least 30 y, in all 27 marine fish stocks addressed by ICES. The stocks and the distributions analysed are listed in Table 1, but for completeness here, the species I investigated were cod (Gadus morhua), Greenland halibut (Reinhardtius hippoglossoides), haddock (Melanogrammus aeglefinus), herring (Clupea harengus), plaice (Pleuronectes platessa), saithe (Pollachius virens), sole (Solea vulgaris), sprat (Sprattus sprattus), and whiting (Merlangius merlangus). The ICES fishing areas, subareas, and divisions for which these stocks are analysed are outlined on the ICES website (http://www.ices.dk/aboutus/icesareas.asp).
Time-series of North Atlantic fish stocks analysed.
| Population by species and ICES areaa . | Mean growth rate〈r〉 . | Standard deviation (σr) . | Year range . |
|---|---|---|---|
| Cod (Gadus morhua) | |||
| 22–24 | − 0.0245 | 0.2899 | 1970–2005 |
| 25–32 | − 0.0183 | 0.2211 | 1966–2005 |
| Northeast Arctic | − 0.0078 | 0.3441 | 1946–2005 |
| Faroe Plateau (Vb1) | − 0.0082 | 0.2147 | 1961–2005 |
| Icelandic (Va) | − 0.0255 | 0.2016 | 1955–2005 |
| VIIa | − 0.0340 | 0.2585 | 1968–2004 |
| Kattegat | − 0.0829 | 0.3210 | 1971–2005 |
| Greenland halibut (Reinhardtius hippoglossoides) | |||
| I and II | − 0.0135 | 0.1636 | 1964–2005 |
| Haddock (Melanogrammus aeglefinus) | |||
| IIIa and IV | 0.0152 | 0.4039 | 1963–2005 |
| Arctic (I and II) | − 0.0004 | 0.3114 | 1950–2005 |
| Faroe (Vb) | 0.0161 | 0.1908 | 1961–2005 |
| Herring (Clupea harengus) | |||
| 25–29 and 32b | − 0.0433 | 0.0865 | 1974–2004 |
| 30 | 0.0313 | 0.1148 | 1973–2004 |
| IIIa, IV and VIIdc | 0.0004 | 0.3244 | 1960–2004 |
| Norwegiand | − 0.0146 | 0.4651 | 1950–2004 |
| VIa | − 0.0074 | 0.2669 | 1957–2005 |
| Plaice (Pleuronectes platessa) | |||
| VIIa | 0.0091 | 0.1509 | 1964–2005 |
| IV | − 0.0072 | 0.1287 | 1957–2005 |
| Saithe (Pollachius virens) | |||
| IIIa, IV and VI | 0.0127 | 0.1512 | 1967–2005 |
| Arctic (I and II) | 0.0194 | 0.1802 | 1960–2005 |
| Faroe (Vb) | − 0.0044 | 0.1051 | 1961–2005 |
| Va | 0.0165 | 0.1387 | 1962–2005 |
| Sole (Solea vulgaris) | |||
| VIIf and g | − 0.0293 | 0.1562 | 1971–2005 |
| VIIe | − 0.0087 | 0.0829 | 1969–2005 |
| IV | − 0.0062 | 0.3483 | 1957–2005 |
| Sprat (Sprattus sprattus) | |||
| 22–32 | 0.0040 | 0.2493 | 1974–2004 |
| Whiting (Merlangius merlangus) | |||
| IV and VIId | − 0.0209 | 0.2088 | 1960–2004 |
| Population by species and ICES areaa . | Mean growth rate〈r〉 . | Standard deviation (σr) . | Year range . |
|---|---|---|---|
| Cod (Gadus morhua) | |||
| 22–24 | − 0.0245 | 0.2899 | 1970–2005 |
| 25–32 | − 0.0183 | 0.2211 | 1966–2005 |
| Northeast Arctic | − 0.0078 | 0.3441 | 1946–2005 |
| Faroe Plateau (Vb1) | − 0.0082 | 0.2147 | 1961–2005 |
| Icelandic (Va) | − 0.0255 | 0.2016 | 1955–2005 |
| VIIa | − 0.0340 | 0.2585 | 1968–2004 |
| Kattegat | − 0.0829 | 0.3210 | 1971–2005 |
| Greenland halibut (Reinhardtius hippoglossoides) | |||
| I and II | − 0.0135 | 0.1636 | 1964–2005 |
| Haddock (Melanogrammus aeglefinus) | |||
| IIIa and IV | 0.0152 | 0.4039 | 1963–2005 |
| Arctic (I and II) | − 0.0004 | 0.3114 | 1950–2005 |
| Faroe (Vb) | 0.0161 | 0.1908 | 1961–2005 |
| Herring (Clupea harengus) | |||
| 25–29 and 32b | − 0.0433 | 0.0865 | 1974–2004 |
| 30 | 0.0313 | 0.1148 | 1973–2004 |
| IIIa, IV and VIIdc | 0.0004 | 0.3244 | 1960–2004 |
| Norwegiand | − 0.0146 | 0.4651 | 1950–2004 |
| VIa | − 0.0074 | 0.2669 | 1957–2005 |
| Plaice (Pleuronectes platessa) | |||
| VIIa | 0.0091 | 0.1509 | 1964–2005 |
| IV | − 0.0072 | 0.1287 | 1957–2005 |
| Saithe (Pollachius virens) | |||
| IIIa, IV and VI | 0.0127 | 0.1512 | 1967–2005 |
| Arctic (I and II) | 0.0194 | 0.1802 | 1960–2005 |
| Faroe (Vb) | − 0.0044 | 0.1051 | 1961–2005 |
| Va | 0.0165 | 0.1387 | 1962–2005 |
| Sole (Solea vulgaris) | |||
| VIIf and g | − 0.0293 | 0.1562 | 1971–2005 |
| VIIe | − 0.0087 | 0.0829 | 1969–2005 |
| IV | − 0.0062 | 0.3483 | 1957–2005 |
| Sprat (Sprattus sprattus) | |||
| 22–32 | 0.0040 | 0.2493 | 1974–2004 |
| Whiting (Merlangius merlangus) | |||
| IV and VIId | − 0.0209 | 0.2088 | 1960–2004 |
Data source: ICES Advice on fish stocks (ACFM Documents from May and October 2005), available at http://www.ices.dk/advice/icesadvice.asp.
aFor ICES fishing areas (including subareas and divisions), see the ICES website (http://www.ices.dk/aboutus/icesareas.asp).
bExcluding Gulf of Riga.
cAutumn spawners.
dSpring spawners.
Time-series of North Atlantic fish stocks analysed.
| Population by species and ICES areaa . | Mean growth rate〈r〉 . | Standard deviation (σr) . | Year range . |
|---|---|---|---|
| Cod (Gadus morhua) | |||
| 22–24 | − 0.0245 | 0.2899 | 1970–2005 |
| 25–32 | − 0.0183 | 0.2211 | 1966–2005 |
| Northeast Arctic | − 0.0078 | 0.3441 | 1946–2005 |
| Faroe Plateau (Vb1) | − 0.0082 | 0.2147 | 1961–2005 |
| Icelandic (Va) | − 0.0255 | 0.2016 | 1955–2005 |
| VIIa | − 0.0340 | 0.2585 | 1968–2004 |
| Kattegat | − 0.0829 | 0.3210 | 1971–2005 |
| Greenland halibut (Reinhardtius hippoglossoides) | |||
| I and II | − 0.0135 | 0.1636 | 1964–2005 |
| Haddock (Melanogrammus aeglefinus) | |||
| IIIa and IV | 0.0152 | 0.4039 | 1963–2005 |
| Arctic (I and II) | − 0.0004 | 0.3114 | 1950–2005 |
| Faroe (Vb) | 0.0161 | 0.1908 | 1961–2005 |
| Herring (Clupea harengus) | |||
| 25–29 and 32b | − 0.0433 | 0.0865 | 1974–2004 |
| 30 | 0.0313 | 0.1148 | 1973–2004 |
| IIIa, IV and VIIdc | 0.0004 | 0.3244 | 1960–2004 |
| Norwegiand | − 0.0146 | 0.4651 | 1950–2004 |
| VIa | − 0.0074 | 0.2669 | 1957–2005 |
| Plaice (Pleuronectes platessa) | |||
| VIIa | 0.0091 | 0.1509 | 1964–2005 |
| IV | − 0.0072 | 0.1287 | 1957–2005 |
| Saithe (Pollachius virens) | |||
| IIIa, IV and VI | 0.0127 | 0.1512 | 1967–2005 |
| Arctic (I and II) | 0.0194 | 0.1802 | 1960–2005 |
| Faroe (Vb) | − 0.0044 | 0.1051 | 1961–2005 |
| Va | 0.0165 | 0.1387 | 1962–2005 |
| Sole (Solea vulgaris) | |||
| VIIf and g | − 0.0293 | 0.1562 | 1971–2005 |
| VIIe | − 0.0087 | 0.0829 | 1969–2005 |
| IV | − 0.0062 | 0.3483 | 1957–2005 |
| Sprat (Sprattus sprattus) | |||
| 22–32 | 0.0040 | 0.2493 | 1974–2004 |
| Whiting (Merlangius merlangus) | |||
| IV and VIId | − 0.0209 | 0.2088 | 1960–2004 |
| Population by species and ICES areaa . | Mean growth rate〈r〉 . | Standard deviation (σr) . | Year range . |
|---|---|---|---|
| Cod (Gadus morhua) | |||
| 22–24 | − 0.0245 | 0.2899 | 1970–2005 |
| 25–32 | − 0.0183 | 0.2211 | 1966–2005 |
| Northeast Arctic | − 0.0078 | 0.3441 | 1946–2005 |
| Faroe Plateau (Vb1) | − 0.0082 | 0.2147 | 1961–2005 |
| Icelandic (Va) | − 0.0255 | 0.2016 | 1955–2005 |
| VIIa | − 0.0340 | 0.2585 | 1968–2004 |
| Kattegat | − 0.0829 | 0.3210 | 1971–2005 |
| Greenland halibut (Reinhardtius hippoglossoides) | |||
| I and II | − 0.0135 | 0.1636 | 1964–2005 |
| Haddock (Melanogrammus aeglefinus) | |||
| IIIa and IV | 0.0152 | 0.4039 | 1963–2005 |
| Arctic (I and II) | − 0.0004 | 0.3114 | 1950–2005 |
| Faroe (Vb) | 0.0161 | 0.1908 | 1961–2005 |
| Herring (Clupea harengus) | |||
| 25–29 and 32b | − 0.0433 | 0.0865 | 1974–2004 |
| 30 | 0.0313 | 0.1148 | 1973–2004 |
| IIIa, IV and VIIdc | 0.0004 | 0.3244 | 1960–2004 |
| Norwegiand | − 0.0146 | 0.4651 | 1950–2004 |
| VIa | − 0.0074 | 0.2669 | 1957–2005 |
| Plaice (Pleuronectes platessa) | |||
| VIIa | 0.0091 | 0.1509 | 1964–2005 |
| IV | − 0.0072 | 0.1287 | 1957–2005 |
| Saithe (Pollachius virens) | |||
| IIIa, IV and VI | 0.0127 | 0.1512 | 1967–2005 |
| Arctic (I and II) | 0.0194 | 0.1802 | 1960–2005 |
| Faroe (Vb) | − 0.0044 | 0.1051 | 1961–2005 |
| Va | 0.0165 | 0.1387 | 1962–2005 |
| Sole (Solea vulgaris) | |||
| VIIf and g | − 0.0293 | 0.1562 | 1971–2005 |
| VIIe | − 0.0087 | 0.0829 | 1969–2005 |
| IV | − 0.0062 | 0.3483 | 1957–2005 |
| Sprat (Sprattus sprattus) | |||
| 22–32 | 0.0040 | 0.2493 | 1974–2004 |
| Whiting (Merlangius merlangus) | |||
| IV and VIId | − 0.0209 | 0.2088 | 1960–2004 |
Data source: ICES Advice on fish stocks (ACFM Documents from May and October 2005), available at http://www.ices.dk/advice/icesadvice.asp.
aFor ICES fishing areas (including subareas and divisions), see the ICES website (http://www.ices.dk/aboutus/icesareas.asp).
bExcluding Gulf of Riga.
cAutumn spawners.
dSpring spawners.
Population fluctuations
Statistical tests rely on the distributions of abundance fluctuations r(t) and their serial correlations over time, in applying a test fit to a Gaussian model, a test of more time, more variation (Lawton, 1988; Inchausti and Halley, 2001, 2002), and a test of draw-downs and -ups (Johansen and Sornette, 1998, 2001) to examine time-series of population fluctuations. One would expect some stocks to grow more slowly than others, resulting in their having less resilience to population decline. To compare different stocks, population variability is standardized by dividing r(t) by its standard deviation σr.
Test 1: distribution of abundance fluctuations

Test 2: time evolution of standard deviation
I here focus attention on the dynamics of the population process, i.e. the serial correlations of abundance fluctuations over time. To do this, I study the population time-series to probe the nature of the stochastic process underlying them, by measuring the time dependence of successive abundance changes.
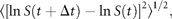
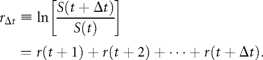
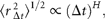
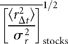
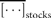 denotes the average across all 27 stocks.
denotes the average across all 27 stocks.Test 3: persistent moves of populations
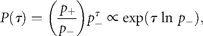
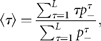
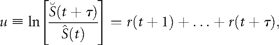
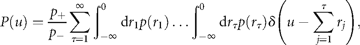
Results
Test for fit to a Gaussian model
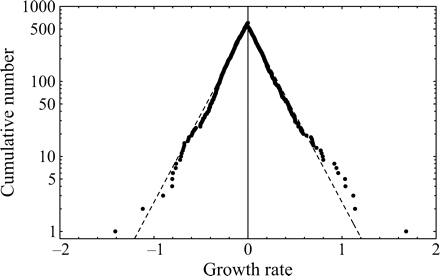
Figure 1a groups the cumulative probability distributions of standardized growth rates [Equation (3)] of 27 fish stocks in the North Atlantic (semi-logarithmic scale plot). The negative and the positive parts are the cumulative and complementary cumulative distributions (cumulative and complementary cumulative numbers are divided by L). The solid lines show the standard normal (complementary) CDFs [Equation (4)]. The values of sample means < r > and standard deviations σrfor individual stocks are given in Table 1; the mean rate of population growth is at the level of noise, < r > ≈0.
Fitting population time-series to a Gaussian model (27 stocks in the North Atlantic, listed in Table 1; data from ICES Advice, ACFM Documents, May and October 2005). (a) Relative number of times a given level of observed population growth rate is plotted against standardized rates r/σrfor each individual stock (semi-logarithmic scale plot). The solid lines show the standard normal (complementary) CDFs [Equation (4)]. (b) Error plot, reading ln[y/PCDF(x)] of data points on (a). (c) Probability density distribution of population growth rates across all 27 stocks (semi-logarithmic scale plot). Standardized data shown in (a) are aggregated, and the solid line shows the standard normal PDF.
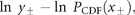
Figure 1c reflects the probability distribution of population growth rate. After binning and averaging the distribution of standardized data (shown in Figure 1a) across all 27 stocks (bin size is 0.25, in units of standard deviation), a quadratic (i.e. parabolic) behaviour on a semi-logarithmic scale is obtained. The aggregated data are well described by the standard Gaussian profile (solid line), the normal PDF with zero mean and unit variance. This result implies that each distribution shown in Figure 1a is symmetrical around r = 0, suggesting that there is no important overall trend in population abundance. Moreover, the fact that mixing distributions with means of zero and identical standard deviations (unity) results in the Gaussian with mean zero and the same standard deviation (unity) is evidence of Gaussian behaviour of each population time-series.
Test for “more time, more variation”
Figure 2(double logarithmic scale plot) shows the width of the distribution functions for the Δt-year growth rate (Δt = 1, 2, …, 20 y); the distribution for time lag Δt = 1 y corresponds to Figure 1c. The standardized statistic [Equation (8)] increases with time lag Δtas in Equation (7), with H = 0.516 ± 0.013 (the adjusted R2, i.e. the coefficient of determination, is calculated, giving R2 = 0.9878); the solid line shows the fit of the linear regression using log-transformed data. This result implies that successive changes in the logarithms of population abundance are not correlated, i.e. the population process is a random process. The mechanism by which the distribution width 〈rΔt2〉1/2evolves is nothing but the consequence of the central limit theorem; the population growth rate r(t) is an iid Gaussian variate. The stochastic process S(t) corresponds to a geometric random walk.
Test for draw-downs and draw-ups
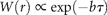
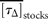 = 2.6 y for draw-downs and
= 2.6 y for draw-downs and 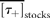 = 2.1 y for draw-ups.
= 2.1 y for draw-ups.Persistent decreases and increases in the population time-series (data from ICES–ACFM Documents of 2005). (a) Complementary CDFs of persistence time (semi-logarithmic scale plot), triangles indicating draw-downs and plus signs draw-ups, and the line depicting the exponential fit to Equation (14), if the draw-downs and -ups are symmetrical. (b) The number of times a given level of draw-downs (triangles) and draw-ups (plus signs) are observed, i.e. complementary CDFs of persistent moves (absolute values) in units of standard deviation, |u|/σr, in a semi-logarithmic scale plot. Here, the solid line shows the symmetrical fit to the exponential CDF [Equation (15)], and the dashed line is the numerical integration of Equation (17) with Equation (12).
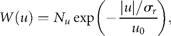
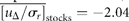 for draw-downs and
for draw-downs and 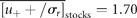 for draw-ups. Fitting the time-series data to Equation (15) yields Nu = 213 and u0 = 1.82 ± 0.07 (adjusted R2 = 0.9730), where the draw-downs and -ups are assumed to be symmetrical for the fit. The mean of consecutive drops in the North Atlantic stocks is given by
for draw-ups. Fitting the time-series data to Equation (15) yields Nu = 213 and u0 = 1.82 ± 0.07 (adjusted R2 = 0.9730), where the draw-downs and -ups are assumed to be symmetrical for the fit. The mean of consecutive drops in the North Atlantic stocks is given by 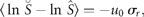
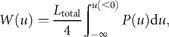
Discussion
Here, I have studied the nature of time-series of exploited North Atlantic fish stocks. What is remarkable about the result shown in Figure 1is that the distribution is, to a good approximation, symmetrical, so that as many populations are increasing in abundance as are decreasing; such a result would be expected for a random process. Both the analysis of runs of successive log-abundance changes (Figure 2) and the persistence statistics (Figure 3) consistently support the statistical independence of series of successive abundance changes; correlations are absent in the exploited population process. Upward and downward steps of the population process are determined by a “fair coin toss”. The exploited population trajectory in logarithms of abundance is a series of the accumulation of random, uncorrelated numbers over time, leading to random-walk dynamics: the running sum of an iid Gaussian variate r(t) is a random walk of ln S(t). This is natural for a stochastic population process, if one considers the annual change of population abundance to be the result of many independent “shocks”, i.e. replenishing (spawning and recruitment of progeny) and mortality from natural (predation and starvation) and human (fishery) causes; the fluctuations r(t) should be Gaussian.
One might suppose that stocks have been under different and varying exploitation regimes and that such stocks exhibit longer-term trends, e.g. that data (on successive abundance changes) in early years of a population's time-series (perhaps a period of general draw-down in a stock) are correlated in time. The empirical results from the ICES–ACFM time-series data are clear evidence against dependence in the successions of annual rates of population growth.
Moreover, one might suppose that each stock has different distributions of r(t) associated with different exploitation regimes in a population time-series: the volatility, σr, of population growth rates would increase with increasing mortality rate, because each year's SSB would, at greater rates of mortality, be based on the contributions of fewer cohorts. Therefore, the distribution of a time-series would exhibit fat-tailed behaviour compared with that of the Gaussian, attributed to mixing of Gaussian distributions with different standard deviations σrat various regimes of exploitation (Allen et al., 2001). The results shown in Figure 1are clear evidence against there being crucial differences in distribution, i.e. that population data records {r(t)} in a time-series are identically Gaussian distributed.
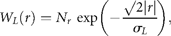
 , and the empirical standard deviation σL = 0.2517. Stock (species and area) differences contribute to differences in the amplitudes of population fluctuations, resulting in an exponential law in population growth-rate distribution when the time-series (unstandardized data) are combined across 27 stocks, and the statistical distribution of time-series values r(t) at various exploitation regimes is the same (i.e. Gaussian) for each stock.
, and the empirical standard deviation σL = 0.2517. Stock (species and area) differences contribute to differences in the amplitudes of population fluctuations, resulting in an exponential law in population growth-rate distribution when the time-series (unstandardized data) are combined across 27 stocks, and the statistical distribution of time-series values r(t) at various exploitation regimes is the same (i.e. Gaussian) for each stock.Mixing Gaussian distributions yields an exponential. The number of times a given level of population growth rate is observed is plotted on a semi-logarithmic scale against unstandardized rates in the combined time-series across the 27 stocks (data from ICES–ACFM Documents of 2005). The dashed line shows the symmetrical fit to Equation (18).
The variance 〈rΔt2〉 of population abundance grows at a rate proportional to the length of the time-series. The finding of the time-series analysis implies that the population process is non-stationary. It has become accepted (cf. Halley, 2005, and references therein) that population variability increases with census length (i.e. the number of years included in the calculation). Such populations are not regulated towards a stable equilibrium point, nor do they have bounded variabilities. The usual theories on harvesting are under a hypothesis of population regulation (e.g. logistic-type or Ricker, 1954, models) with the replacement line; they imply the existence of an equilibrium point to which the population is attracted, or a “basin of attraction” wherein population abundance is constrained to lie (Beverton and Holt, 1957; Turchin, 1999). There is now some doubt whether populations are persistent in growing (or declining) on a path to equilibrium, which is the usual assumption in fisheries management (Steele and Henderson, 1984). The dynamics of exploited stocks result in a random walk down the population path.
I have here examined the variance of population fluctuations and the persistent duration and magnitude of population moves over time on North Atlantic commercial fish stocks. There is yet another approach to the problem of stationarity and population regulation. It may be valuable to examine frequency variations (the variance per unit frequency interval, in units of y−1) of exploited population time-series, i.e. the spectra of population fluctuations, to investigate whether exploited populations are moving non-stationarily (low-frequency variability has greater amplitude than high-frequency variability, corresponding to unregulated non-equilibrium dynamics) or whether the population process S(t) contains equal-amplitude components of the spectrum at all frequencies (the population spectrum is white noise, corresponding to the extreme case of tight regulation).
In exploited fish populations, time-series analysis of landings has provided empirical evidence against stationarity (Halley and Stergiou, 2005). Besides the random nature of escapement from a fishery (i.e. SSB time-series), it is necessary to examine the statistical properties of the manner in which landed catches from fishing a stock change over time. Because the future harvest from a fish stock is uncertain, the relationship between the escapement of catchable adults from a fishery in one year and landing streams in future is of great importance.
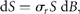
Acknowledgements
I thank two anonymous reviewers for their constructive comments on two draft versions of the manuscript, and editor Andrew Payne for his encouragement.



![Fitting population time-series to a Gaussian model (27 stocks in the North Atlantic, listed in Table 1; data from ICES Advice, ACFM Documents, May and October 2005). (a) Relative number of times a given level of observed population growth rate is plotted against standardized rates r/σrfor each individual stock (semi-logarithmic scale plot). The solid lines show the standard normal (complementary) CDFs [Equation (4)]. (b) Error plot, reading ln[y/PCDF(x)] of data points on (a). (c) Probability density distribution of population growth rates across all 27 stocks (semi-logarithmic scale plot). Standardized data shown in (a) are aggregated, and the solid line shows the standard normal PDF.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/icesjms/64/3/10.1093_icesjms_fsm004/1/m_fsm00401.gif?Expires=1716561315&Signature=mEXC4aBwd-vi6nfHINzXmUSmsYwiRIjbMMO87VtGnerFbK6OUCjbjBZJdAn3yjmg1cuG77KDU3TVuNJqUCZhgNZW~uWoCI~vf3mAfEcr4~t7~49XjXT6w-bezxGmMx0LRJc8sof~BtckIOxR0VmnKSCA8gCqVycouDnTzsZiuhJGrhSOQdHdWgS8WYM6GUbs4ePp4-b~kVi-1fdX-gz0-0QtOLeBG8OgfJEFqpOG7y~bMi2KB1Z3fq8hb34WJKP-iuXChNO7siz1x2QJK5XAYfdZJtKlZtSGfd3xbrkoeqfITP8IyEopgPiv1hZYtA1TJYS3j8gFs98Uqv2PEaOPIg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
![Characterization of abundance moves in the population time-series (data from ICES–ACFM Documents of 2005), in a double logarithmic scale plot. Dots show the standard deviations of Δt-year growth rates (rΔt/σr) across all 27 stocks [Equation 8], and the solid line is the fit to Equation (7).](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/icesjms/64/3/10.1093_icesjms_fsm004/1/m_fsm00402.gif?Expires=1716561315&Signature=ya1dqHeT0yuMXM4Xb6qKGwfusJVE49w4FSiVMwdLTyosoDysRMXrjE2x-Bc4W5gRA23tT0zC~~0vI-7uK8TJPu9izjhqNoHVyfjoo2DFqRFv-sRlRIZg3cskjyXOfFR7tlk~r-pcsR9Zdwhvgz~5MGdEjrHcnwDOZ0cBvk4g60zRsb6Xwp5pChK9G8IX7XIKT~PVArrMTCkgggc1s2Ysh3LlT3prSa73e06P5VXB8LswMrIHixzLzJZ2hrBmLNM6xvle2D5uOy41EAzfNFaL9wMcr-0KNwhIu93TK0xwng3HUUnvhOLfCDeReqHfejzA06cGAb7OwznscJCh~WGODQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
![Persistent decreases and increases in the population time-series (data from ICES–ACFM Documents of 2005). (a) Complementary CDFs of persistence time (semi-logarithmic scale plot), triangles indicating draw-downs and plus signs draw-ups, and the line depicting the exponential fit to Equation (14), if the draw-downs and -ups are symmetrical. (b) The number of times a given level of draw-downs (triangles) and draw-ups (plus signs) are observed, i.e. complementary CDFs of persistent moves (absolute values) in units of standard deviation, |u|/σr, in a semi-logarithmic scale plot. Here, the solid line shows the symmetrical fit to the exponential CDF [Equation (15)], and the dashed line is the numerical integration of Equation (17) with Equation (12).](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/icesjms/64/3/10.1093_icesjms_fsm004/1/m_fsm00403.gif?Expires=1716561315&Signature=jTVT51crngNlJOd1ekkZzV1QIvcMMf8VwVyHOiPnu5OHPWdF7angf6V7518ucWrzqzmzicLnYOeWBP5vSUFgBdOW1EQvZxTDGPQXK9tz-hfYdCxg8JBH9VH2x31hzyLx~B8ChTx0vmdRa1EWK3XKVxGBRD2m4khITojLVRBI9h01xxhcgHrLar~K0OJk5LxMWkPbHHcQnS~4APh5EmAE1p-ei47cmWmQrjh9ItrbY0xZu6GLWe6oBez6qQbPDzUYVZ6iiPw7bDQmEoemhhSXYoJTUm3566106NtSQD0RmLNbpPcl0hais-XZPU6uFPFUaFzt7J6VoVXli24e8n7rvg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)